Die Reproduktionszahl R wird häufig als Indikator verwendet, um vorauszusagen, wie schnell sich eine Infektionskrankheit in der Gesellschaft ausbreitet. Empa-Forschende haben ein mathematisches Modell entwickelt, das ebenso einfach anzuwenden ist wie R, aber genauere Vorhersagen ermöglicht. Ihr Modell setzt auf eine «Reproduktionsmatrix», die der Heterogenität der Gesellschaft Rechnung trägt.
«Deine Freunde haben mehr Freunde als du», schrieb der US-amerikanische Soziologe Scott Feld 1991. Felds sogenanntes «Freundschaftsparadox» besagt, dass die Freunde einer beliebigen Person im Durchschnitt mehr Freunde haben als die Person selbst. Dahinter steckt eine einfache Wahrscheinlichkeitsrechnung: Gut vernetzte Menschen tauchen mit einer höheren Wahrscheinlichkeit in den Freundeskreisen anderer auf.
«Wenn man den Freundeskreis einer beliebigen Person betrachtet, ist es sehr wahrscheinlich, dass in diesem Freundeskreis sehr gut vernetzte Personen mit überdurchschnittlich vielen Freunden vorkommen», erklärt Empa-Forscher Ivan Lunati, Leiter des Labors «Computational Engineering». Ein ähnliches Prinzip diente Lunati und seinem Team als Grundlage für ein neues mathematisches Modell, mit dem sich die Entwicklung von Fallzahlen während einer Epidemie genauer vorhersagen lässt.
Doch was haben Freundeskreise mit Infektionskrankheiten zu tun? «Je mehr Kontakte eine Person hat, desto mehr Menschen kann sie in einer Epidemie anstecken», erklärt Lunati. Herkömmliche epidemiologische Modelle gehen aber davon aus, dass jede infizierte Person im Verlauf der Epidemie im Durchschnitt gleich viele andere Personen ansteckt. Diese Anzahl wird als Reproduktionszahl (R) bezeichnet. Ist R grösser als eins, steigen die Fallzahlen exponentiell an; ist R kleiner als eins, sinken sie.
Natürlich ist dieses Modell vereinfacht: «Die Fallzahlen können nicht unendlich weitersteigen, da die Bevölkerung nicht unendlich gross ist», so Lunati. Das rasante exponentielle Wachstum finde vor allem zu Beginn einer Welle statt, so der Forscher. Mit der Zeit gibt es immer weniger Menschen, die noch angesteckt werden können, der R-Wert nimmt also ab, und die Zunahme der Neuinfektionen verlangsamt sich, bis es schliesslich zu einem Infektions-Peak kommt und die Fallzahlen wieder zu sinken beginnen – eine Kurve, die nach der Covid-Pandemie wohl den meisten Menschen vertraut ist.
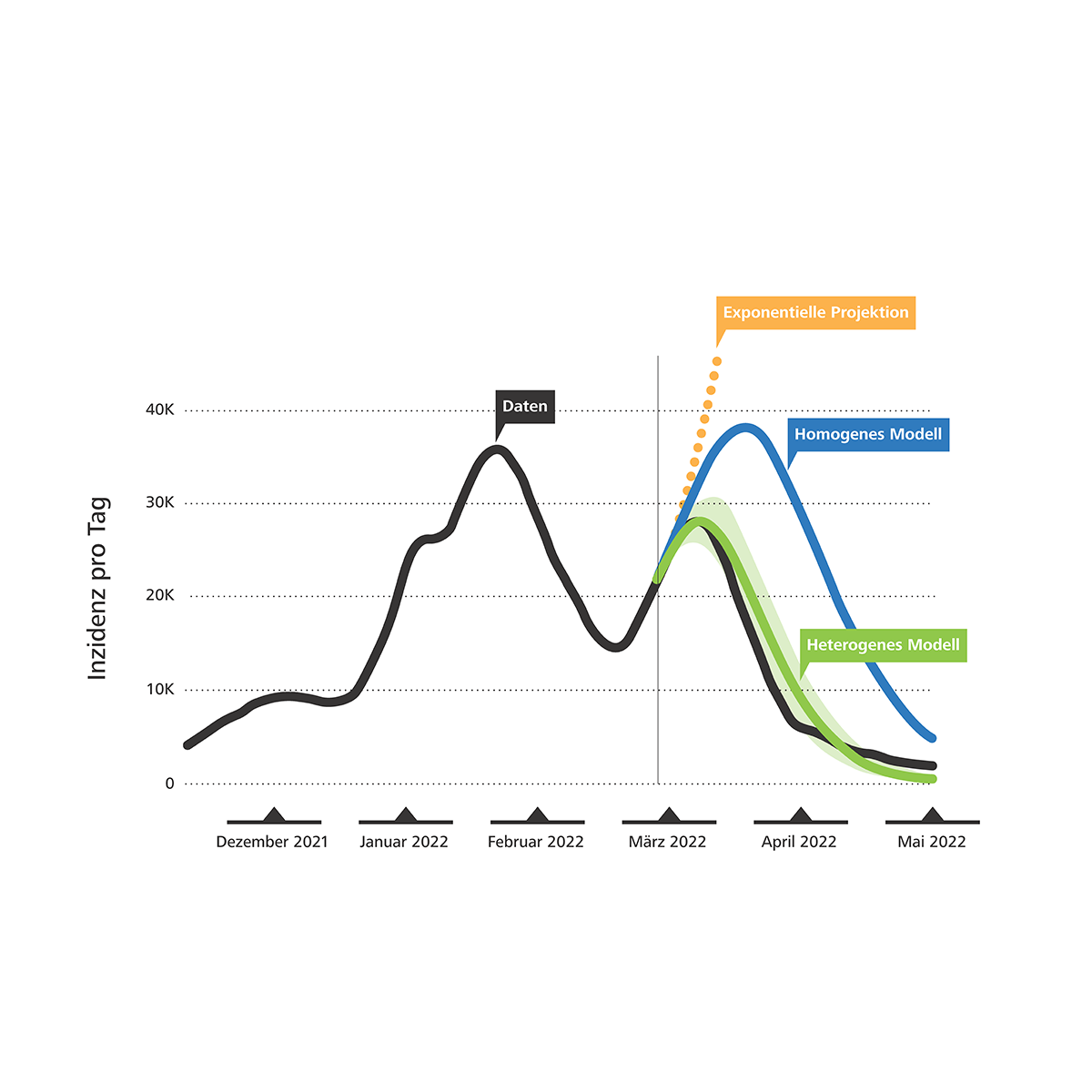
Infektion: Nicht unendlich viele «Superspreader»
Diese Infektionskurve lässt sich mit mathematischen Methoden berechnen, um ihren Peak vorherzusagen. Geht man dabei von der Annahme aus, dass jede infizierte Person gleich viele andere Menschen ansteckt, weicht das Modell jedoch von den empirisch gemessenen Infektionswellen ab. Zwar kann es den Beginn der Welle gut wiedergeben, im späteren Verlauf ebbt die Infektionswelle jedoch schneller ab als vorhergesagt jedoch schneller als vorhergesagt, sodass der Peak schlussendlich etwas tiefer ausfällt als in der Modellrechnung – und zwar selbst dann, wenn keine neuen Schutzmassnahmen den Infektionsverlauf beeinflussen.
Gemeinsam mit dem Empa-Forscher Hossein Gorji sowie Noé Stauffer, Doktorand an der Empa und der EPFL, stellte sich Lunati die Frage: Wie machen wir solche Vorhersagen genauer? Ihre Antwort hat Parallelen mit dem Freundschaftsparadox. «Menschen mit vielen sozialen Kontakten stecken sich besonders schnell an, und stecken ihrerseits wieder viele andere an», erklärt Lunati. Solche Menschen bezeichnen die Forschenden auch als Hubs oder Superspreader. Zu Beginn einer Infektionswelle sind es vor allem sie, die den Anstieg der Fallzahlen vorantreiben. Die Anzahl solcher Superspreader in der Gesellschaft ist allerdings relativ klein. Sind sie alle infiziert – was aufgrund ihrer vielen Kontakte relativ schnell eintrifft –, verlangsamt sich die Ausbreitung der Krankheit. Herkömmliche Modelle, die auf der Reproduktionszahl R basieren, berücksichtigen diese Verlangsamung nicht.
In einer Studie, die vor kurzem im «Journal of the Royal Society Interface» veröffentlicht wurde, schlagen Gorji, Stauffer und Lunati deshalb die Verwendung einer sogenannten Reproduktionsmatrix anstelle der Reproduktionszahl vor. Diese Matrix sagt aus, wie schnell einzelne Bevölkerungsgruppen angesteckt werden, und trägt somit der Heterogenität der Gesellschaft Rechnung. «Wir wollten über die vereinfachte Interpretation der Reproduktionszahl R hinausgehen und die Komplexität realer Epidemiewellen besser erfassen,» so Hossein Gorji. «Die Reproduktionsmatrix ermöglicht uns eine genauere Vorhersage der Krankheitsausbreitung, indem sie sowohl die Nichtlinearität als auch die Heterogenität berücksichtigt, die bei herkömmlichen Modellen oft übersehen werden.» Das Forschungsprojekt wurde vom Schweizerischen Nationalfonds (SNF) unterstützt.
Auch für andere Netzwerke
Bei der Definition dieser Reproduktionsmatrix setzten die Forschenden auf Daten aus anderen Studien. Für ihr Modell teilten sie die Gesellschaft nach Alter in Gruppen ein. Am meisten Kontakte haben dabei – im Durchschnitt – Personen zwischen 10 und 25 Jahren. «Diese Gruppeneinteilung nach Alter ist natürlich eine Verallgemeinerung, echte soziale Kontakte sind komplexer», erklärt Lunati. «Ausserdem nimmt unser Modell an, dass sowohl die Ansteckungen als auch die Superspreader gleichmässig im ganzen Land verteilt sind. Für kleine Länder mit gut verbundenen Regionen und relativ einheitlichen sozialen Strukturen ist diese Annahme wenig problematisch. Bei grossen Ländern müssten wir aber auch die geografische Verteilung der Bevölkerung und die Kontakte zwischen den Regionen berücksichtigen.»
Ihr neues Modell testeten die Forscher mit Covid-Daten aus der Schweiz und aus Schottland – beides relativ kleine Länder. Sie konnten zeigen, dass die Matrix wesentlich genauere Vorhersagen von Infektions-Peaks ermöglicht. «Natürlich ist auch unser Modell stark vereinfacht», sagt Lunati. Die Stärke des Matrix-Modells liegt aber gerade in seiner Einfachheit: «Es ist sehr einfach anzuwenden, aber zugleich viel realistischer als der R-Wert allein.»
Die Nützlichkeit des neuen Modells beschränkt sich dabei nicht auf Epidemien: Es kann in unterschiedlichen Systemen zum Einsatz kommen – immer dann, wenn sich Objekte über ein Netzwerk verbreiten. So wollen es die Forschenden künftig etwa verwenden, um die Ausbreitung von Ansichten, Meinungen und Verhaltensweisen in einer Gesellschaft zu simulieren – etwa, wenn es um die Adoption von neuen Technologien oder einer nachhaltigen Lebensweise geht.







